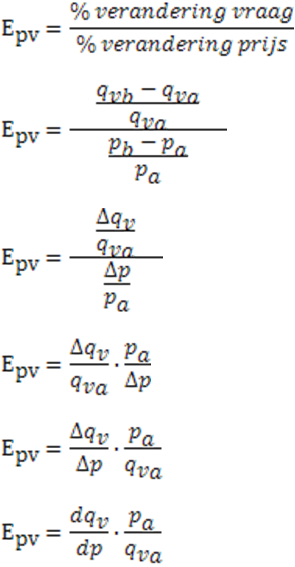Wanneer je een elasticiteit moet uitrekenen zonder dat er iets verandert, mag je eigenlijk niet de ‘normale’ formule gebruiken. Deze formule gaat uit van procentuele veranderingen, die er dan niet zijn.
Beschreven verandering: segmentberekening
Bij deze berekening gaan we ervan uit dat er een verandering plaats vindt.
Bijvoorbeeld bij de prijselasticiteit:
 Qv = -25P + 1.000
Qv = -25P + 1.000
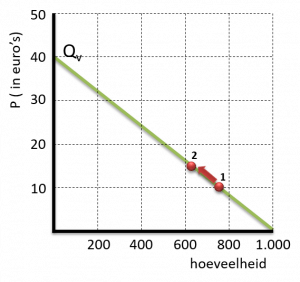
Wanneer de prijs (oorzaak) van € 10 naar € 15 gaat,
zal de vraag van 750 naar 625 gaan.
![]()
10→15 × Ev = 750→625
+50% × Ev = -16,67%
Ev = -0,33
Omdat we een stukje over de lijn verschuiven, spreken we van een segmentberekening.
Geen verandering: zelf verzinnen
Het komt ook voor dat er geen verandering is beschreven. In dat geval moet de elasticiteit in één vast punt berekend worden.
Zolang er sprake is van een rechtlijnig verband, mag je gewoon zélf een verandering vanuit het gevraagde punt verzinnen.
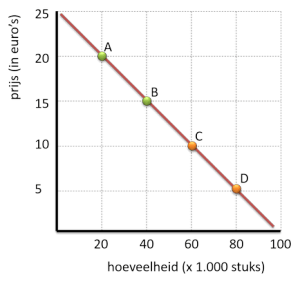
Bijvoorbeeld wanneer we de prijselasticiteit bij een prijs van € 20 moeten uitrekenen, dus in punt A:
In punt A geldt een prijs van € 20 en een hoeveelheid van 20.
We verzinnen een prijsdaling van € 1 ten opzichte van € 20 = -5%
Een vraagtoename van 4 ten opzichte van 20 = +20%
⇒ Ev = -4
Maar wanneer je een andere prijsdaling verzint,
zoals € 15 ten opzichte van € 20 = -75%
Zal de vraagtoename 60 zijn ten opzichte van 20 = +300%
⇒ Ev = -4
Beide veranderingen leveren dezelfde elasticiteit op.
EIS: het vertrekpunt (oud) is het punt waarvoor je de elasticiteit moet uitrekenen.
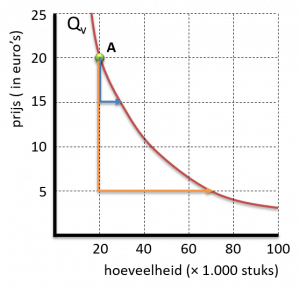
Een kromme zou een beter beeld geven van de werkelijke verhouding tussen prijs en vraag.
Wanneer we nu vanuit punt A zelf een verandering verzinnen, krijgen we helaas niet meer dezelfde elasticiteit eruit.
BLAUWE pijl:
Prijs daalt van € 20 naar € 15 ⇒ -25%
Vraag stijgt van 20 naar 30 ⇒ +50%
Dat levert op: Ev = -2
ORANJE pijl:
Prijs daalt van € 20 naar € 5 ⇒ -75%
Vraag stijgt van 20 naar 70 ⇒ +250%
Dat levert op: Ev = -3,3
Géén verandering beschreven: puntberekening
Zoals we in bovenstaand voorbeeld hebben gezien is het gebruiken van een segmentberekening met een verzonnen verandering in een vast punt dus eigenlijk niet helemaal correct.
We moeten niet zomaar een verandering verzinnen, maar de verandering gebruiken IN dat punt. Dat betekent dat we de helling van de raaklijn in dat punt moeten gebruiken.
Voor de prijselasticiteit van de vraag krijgen we dus de volgende formule:
Stel: Qv = -20P + 500
Gevraagd: de prijelasticiteit bij een prijs van € 10 (en een vraag van 300)
In het eerste deel van de formule wordt de helling van de raaklijn gevraagd.
is in dit geval dus de helling van de vraaglijn = -20
In het tweede deel van de formule gaat het om de waarden van het punt.
Dus p=10 en qv= 300
Wanneer we de formule voor de puntberekening van de prijselasticiteit nogmaals bekijken, kunnen we de formule gemakkelijk ombouwen voor andere elasticiteiten.
Het eerste deel vraagt naar de mate waarin het gevolg op de oorzaak reageert IN het betreffende punt.
Het tweede deel vermenigvuldigt deze mate van reactie met de waarden VAN het punt, zodat de absolute verandering relatief gemaakt wordt.