Een voorbeeld van toepassing van de speltheorie is het zogenaamde prisoners dilemma of gevangenenprobleem.
Bij een prisoners dilemma ontstaat een Nash-evenwicht dat niet optimaal is. Eenzijdig handelen kan de uitkomst niet verbeteren, maar door samenwerking zou een betere uitkomst tot stand kunnen komen.
Het klassieke voorbeeld van het gevangenenprobleem
Situatie:
- Eduard de Roos is vermoord
- twee verdachten: Theo G. en Mohammed V.
- bij aanhouding droegen zij een wapen, zonder wapenvergunning
- één van de verdachten is vermoedelijk de dader
- er is genoeg bewijs voor 2 jaar cel voor verboden wapenbezit
- bekentenis is nodig om de moord op te lossen
Werkwijze politie:
- verdachten worden apart verhoord (er is dus géén overleg mogelijk tussen de verdachten)
- voorgelegde keuze: zwijgen of de ander aangeven
- als beiden zwijgen moeten beiden 2 jaar de gevangenis in voor verboden wapenbezit
- als je als enige de ander aangeeft ga je vrijuit en krijgt de ander 14 jaar cel
- als ze beiden de ander aangeven, moeten beiden 10 jaar de cel in (omdat niet bewezen kan worden wie er geschoten heeft)
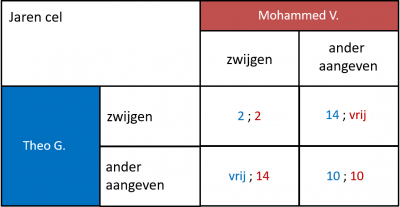
Deze hele situatie kunnen we in een opbrengstenmatrix zetten:
De beste reactie van Mohammed V.:
- wanneer Theo zwijgt, kan ik hem het beste aangeven: vrij is beter dan 2 jaar de cel in
- wanneer Theo me aan geeft, kan ik hem het beste óók aangeven: 10 jaar cel is beter dan 14 jaar cel
De beste reactie van Theo G.:
- wanneer Mohammed zwijgt, kan ik hem het beste aangeven: vrij is beter dan 2 jaar cel
- wanneer Mohammed me aan geeft, kan ik hem het beste óók aangeven: 10 jaar cel is beter dan 14 jaar cel
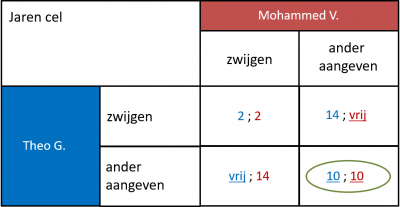
Wanneer we dat verwerken in de opbrengstenmatrix, kunnen we het Nash-evenwicht vinden:
Beide spelers hebben een dominante strategie: de ander aangeven.
Hierdoor is het Nash-evenwicht niet optimaal.
Veel beter was het geweest als ze allebei gezwegen hadden. Dan was de gezamenlijke opbrengst veel beter.
Dit niet-optimale Nash-evenwicht is hét kenmerk van een prisoners dilemma.
Een economisch prisoners dilemma
Twee kledingzaken in een winkelcentrum moeten beslissen of zij wél of niet beginnen met een vervroegde uitverkoop.
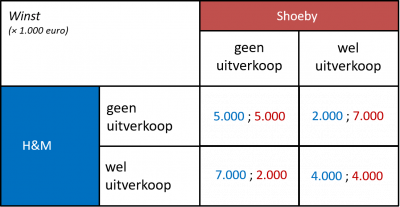
Deze keuze en de daarbij behorende opbrengsten staan in onderstaande opbrengstenmatrix.
De beste reactie van Shoeby:
- wanneer H&M geen uitverkoop houdt, kan ik het beste wél een uitverkoop houden:
€ 7.000 is beter dan € 5.000 - wanneer H&M wél uitverkoop houdt, kan ik het beste óók uitverkoop houden:
€ 4.000 is beter dan € 2.000
De beste reactie van H&M:
- wanneer Shoeby geen uitverkoop houdt, kan ik het beste wél een uitverkoop houden:
€ 7.000 is beter dan € 5.000 - wanneer Shoeby wél uitverkoop houdt, kan ik het beste óók uitverkoop houden:
€ 4.000 is beter dan € 2.000
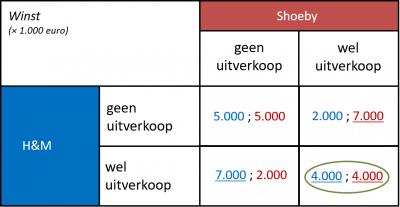
Wanneer we dat verwerken in de opbrengstenmatrix, kunnen we het Nash-evenwicht vinden:
Eenzijdig kan geen van beide winkels haar winst verbeteren. Gezamenlijk wél!
Oplossingen
Om tot een optimale uitkomst te komen moeten beide partijen samenwerken. Vertrouwen en geloofwaardigheid zijn dan natuurlijk belangrijk om er zeker van te zijn dat de ander zich houdt aan de afspraken.
Zoiets kan natuurlijk bevorderd worden door het opstellen van contracten, maar dat mag niet altijd. Bijvoorbeeld door geldende kartelwetgeving, die verbiedt dat bedrijven afspraken maken waarmee zij de consument benadelen.
Oplossingen kunnen zijn: