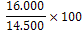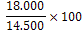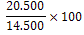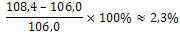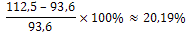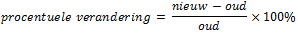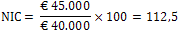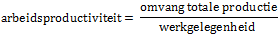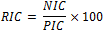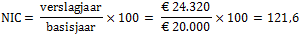Vraag 1
De onderstaande tabel geeft een overzicht van de gemiddelde prijzen (in euro’s) van een auto in de afgelopen jaren.
|
jaar
|
1990
|
1995
|
2000
|
2005
|
2010
|
2015
|
|
gemiddelde prijs (€)
|
14.500
|
16.000
|
18.000
|
20.500
|
22.000
|
25.000
|
| a | Zet bovenstaande prijzen om in indexcijfers met als basisjaar 1990. |
Vraag 2
Gegeven de ontwikkeling van het consumenten prijsindexcijfer:
|
jaar
|
2012
|
2013
|
2014
|
2015
|
2016
|
2017
|
|
CPI
|
93,6
|
100,0
|
103,2
|
106,0
|
108,4
|
112,5
|
| a |
Bereken de procentuele verandering van de prijzen in 2016 (ten opzichte van 2015). Afronden op twee decimalen. |
| b |
Bereken de procentuele verandering van de prijzen in de periode 2012 – 2017. Afronden op twee decimalen. |
| c |
Bereken de nieuwe reeks met indexcijfers indien 2015 het nieuwe basisjaar wordt. |
Vraag 3
| a |
Van de consumentenprijzen is gegeven dat: CPI2015 = 145 ⇒ Met hoeveel procent is het algemene prijspeil in deze periode veranderd? Afronden op één decimaal. |
| b |
Iemand verdient in 2012 een nominaal inkomen van € 40.000. De prijzen zijn in 2017 t.o.v. 2012 met 9,7% gestegen. ⇒ Met hoeveel procent is het reëel besteedbaar inkomen in 2017 veranderd t.o.v. 2012? Afronden op één decimaal. |
| c |
Het CPI stijgt van 110 tot 135. ⇒ Bereken met hoeveel procent de koopkracht van het geld is veranderd door deze prijsstijging. Afronden op één decimaal. |
| d |
Iemand leent in 2015 € 5.000 van de bank. ⇒ Bereken de procentuele afname van de koopkracht van deze € 5.000 als dit bedrag (zonder rente) na afloop van de uitleentermijn wordt terugbetaald. Afronden op één decimaal. |
| e |
De bank vraag voor een lening een nominale rente van 5,5% ⇒ Bereken de reële rente die de bank voor de lening vraagt. |
Vraag 4
We nemen 2005 als basisjaar.
De lonen stijgen in de periode 2005- 2010 met 12%.
De lonen stijgen in de periode 2010 – 2015 met 5%.
De prijzen stijgen in de periode 2005 – 2010 met 8,5%.
De prijzen dalen in de periode 2010 – 2015 met 1,5%.
Meneer X heeft een vaste nominale uitkering die in het basisjaar € 2000 bedraagt.
Meneer Y heeft een waardevaste uitkering die in het basisjaar € 2000 bedraagt.
Meneer Z heeft een welvaartsvaste uitkering die in het basisjaar € 2000 bedraagt.
| a |
Bereken de nominale bedragen die de drie heren in 2010 ontvangen. |
| b |
Bereken met hoeveel procent de reële inkomens van elk van deze drie heren in de periode 2005- 2010 is veranderd. |
| c |
Bereken met hoeveel procent het reële inkomen van meneer Z in de hele priode 2005-2015 is veranderd. |
Vraag 5
| a |
Een producent van computersoftware verhoogt zijn prijs met 5%. Als reactie daarop neemt de omzet met 3% af. ⇒ Bereken met hoeveel procent zijn afzet is gedaald. |
| b |
De productie van een kaasfabrikant neemt met 5% toe. Hiervoor moet hij 2% extra arbeidskracht inhuren. ⇒ Bereken de procentuele verandering van de arbeidsproductiviteit. Afronden op twee decimalen. |
| c |
De arbeidsproductiviteit in een productiebedrijf is het afgelopen jaar met 6% gestegen. ⇒ Bereken de procentuele verandering van de werkgelegenheid in dit bedrijf. Afronden op twee decimalen. |
| d |
De werkgelegenheid in een bedrijf stijgt 3 jaar lang jaarlijks met 2%. ⇒ Bereken de procentuele verandering van de arbeidsproductiviteit na deze 3 jaren. Afronden op één decimaal. |
| e |
Iemand verdient in 2010 € 20.000. In 2015 neemt dit inkomen toe tot € 24.320. ⇒ Met hoeveel procent is het reëel inkomen van deze persoon veranderd? Afronden op één decimaal. |