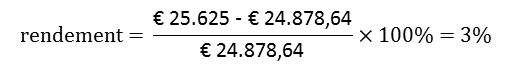Op 15 juni 2013 geeft de Nederlandse overheid de volgende obligatielening uit:
De marktrente is in juni 2013 zo’n 1,8%
Marinda wil de obligatie wel kopen met haar spaargeld.
| a |
Leg, zonder een berekening, uit welk rendement Marinda zal halen uit haar belegging indien zij nu de obligatie koopt en hem daarna niet meer doorverkoopt. Verklaar je antwoord. |
| b |
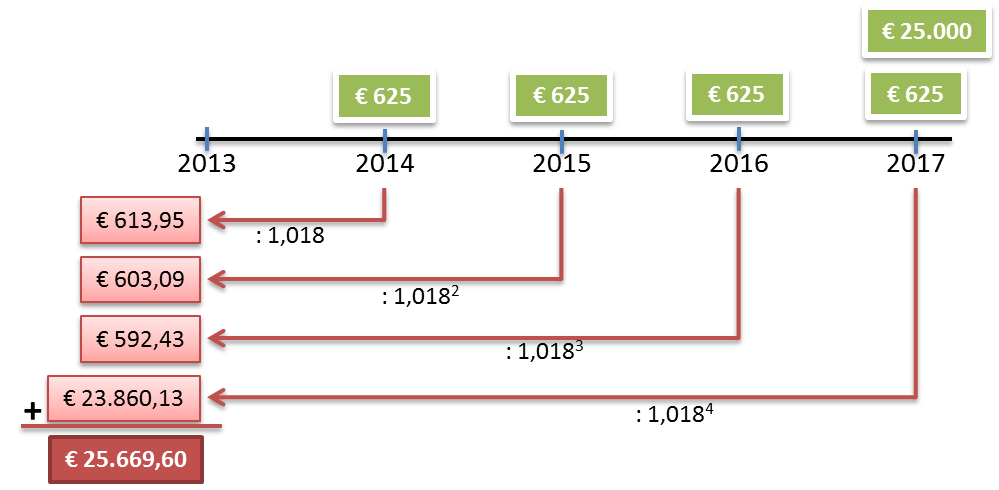
Bereken hoeveel Marinda zal moeten betalen voor deze obligatie op 15 juni 2013. |
| c |
Bereken de uitgiftekoers van deze obligatie op 15 juni 2013. |
Op 16 juni 2016, direct na ontvangst van de jaarlijkse couponrente, verkoopt Marinda haar obligatie. Zij ontvangt hiervoor nog maar een bedrag van € 24.878,64
| d |
Bereken hoeveel rendement Marinda nu uiteindelijk heeft behaald met haar belegging. |
| e |
Verklaar dit rendement. |
| f |
Bereken de hoogte van de marktrente in juni 2016. |
| a |
De obligatie is aantrekkelijker dan sparen bij de bank. Er zal dus veel vraag naar zijn. Daarom zal de prijs stijgen. Uiteindelijk zal er zoveel voor betaald moeten worden dat het rendement gelijk wordt aan het rendement bij het sparen: 1,8% |
| b |
Om uit te rekenen wat iemand maximaal wil betalen voor de obligatie, moet je kijken wanneer het rendement van de obligatie gelijk wordt aan een belegging tegen de marktrente.
|
| c |
|
| d |
Zij heeft de obligatie gekocht voor € 25.669,60 en verkocht voor € 24.878,64. Dat was een verlies van € 790,96 In totaal was haar ‘winst’ dus: (3 × 625) – 790,96 = € 1.084,04 over 3 jaar Dat is zo’n € 361,35 per jaar. Met een belegging van € 25.669,60 is dat een rendement van 1,41% |
| e |
Blijkbaar is de marktrente in de loop van de jaren gestegen. Daardoor is voor kopers deze obligatie niet meer aantrekkelijk. Hij levert weinig op in de verkoop. Daardoor daalt voor Marinda het rendement. |
| f |
Iemand betaalt nu € 24.878,64 in de wetenschap dat hij over één jaar € 25.625 gaat krijgen.
|
